变压器

变压器的基本原理和结构

变压器的基本原理

电源变压器
环形变压器
接触调压器
控制变压器

基本工作原理

以磁场为媒介，通过电磁感应作用，把一种电压的交流电转化成另一种相同频率电压的交流电。

关键词

磁场，电磁感应，电压，交流电，相同频率

最关键的两个点：

只有通交流电才能工作
两个绕组匝数不同，电压就不同

变压器的基本结构

磁路部分：铁芯(core)

通过电工钢片叠压而成的闭合磁路

叠片的目的：减少涡流

电路部分：绕组(winding)

原边线圈（一次侧）AX，次边线圈（二次侧）ax。

变压器的额定值

使用变压器的时候，必须满足一定的条件。

额定容量 $S_N$

输入的电压和电流的乘积。

额定电压 $U_N$

一次侧：输入的电压。二次侧：一次侧额定时，负载端空载时的电压（电势）。

三相变压器中，指的是线电压。（所有的额定参数指的都是线参数）

额定电流 $I_N$

单相： $$ S_N=U_NI_N $$ 三相： $$ S_N=\sqrt{3}U_NI_N $$

连接组号：三相变压器特有。

变压器分析的两个基础

理想变压器

变压器的运行过程：

一次侧加电压，电流流过导线，因为导线有电阻，所以产生铜损（电机学中的习惯叫法）。

电流产生磁势，所以就会产生主磁通和漏磁通，而交变的磁通会在铁芯中产生涡流，这就是铁损。

二次侧的电流流过导线，也会产生铜损。

总结

铜损，铁损，磁漏

主磁通和漏磁通的区别

作用不同：
主磁通传递能量，交链原边和副边；
漏磁通只消耗磁动势，只起到磁压降作用。
特性不同：
主磁通和电流是非线性关系（介质是铁芯）
漏磁通和电流是线性关系（介质是空气）

正方向原则

一般采用电动机惯例。

电压方向决定电流方向。
电流方向决定磁通方向（右手）。
磁通方向决定电势方向（右手）。

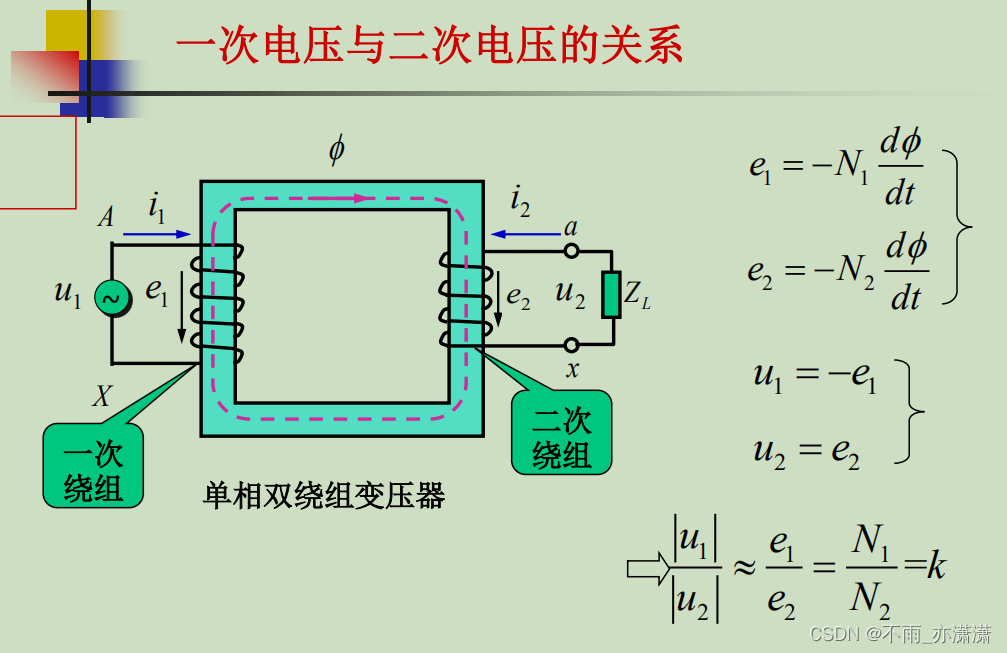
变压器参考方向

关键

电流方向和电势方向一致。

变压器空载运行时的方程式

稳态电压平衡： $$ \dot{U_1}=-\dot{E_1}-\dot{E_{1\sigma}}+\dot{I_0}r_1 $$

空载电流 $\dot{I_0}$

空载电流一般是电流的2%~10%。空载不太费电。
电压为正弦波的时候，电流为尖顶波。因为磁路饱和。

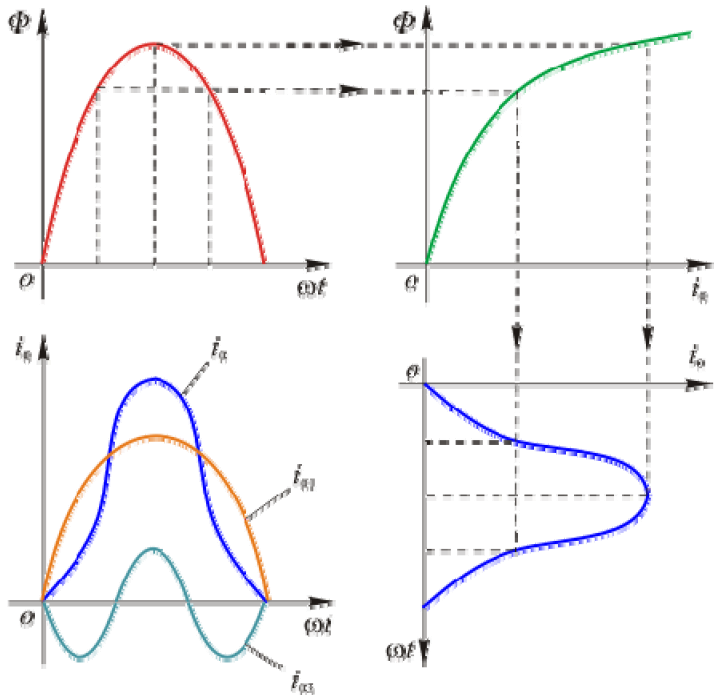
磁路饱和时电压和电流波形解释

相位：空载电流与主磁通同相，但是超前一个$\alpha$角，$\alpha$是铁损角。
可以把空载电流分解为与主磁通同相的分量和与主磁通正交的分量。同相的分量称为磁化电流$i_\mu$，正交的分量称为铁损分量$i_{Fe}$。
这里的物理意义是什么？
为什么是超前？

认为主磁通按照正弦规律变化： $$ \phi=\phi_m\sin(\omega t) $$ 则电动势为： $$ E_1=-N_1\frac{d\phi}{dt}=-N_1\omega\phi_m\cos(\omega t)=E_{1m}\sin(\omega t - 90°) $$ 4.44公式： $$ E_1=4.44f_1N_1\phi_m $$ 为什么左边是有效值，右边是峰值？因为4.44比较好记。

主电势滞后于主磁通90°。同时，需要注意主电动势和主磁通是垂直的，而空载电流会和主磁通有一点角度差。

原边的漏电抗：

\[ \begin{align*} \dot{E_{1\sigma}} & = -j\omega L_{1\sigma}\dot{I_0}\\ x_{1} & = \omega L_{1\sigma} \end{align*} \]

变压器的电压平衡方程式（空载）

\[ \begin{align*} \dot{U_{10}} & = -\dot{E_1}+\dot{I_0}Z_1\\ \dot{U_{20}} & = \dot{E_2} \end{align*} \]

其中，我们称$Z_1$为原边绕组漏阻抗。从数值上来看，漏阻抗的压降很小，所以电压主要和电势相平衡。

关键

变压器的主磁通主要取决于电网电压，频率和匝数，与负载大小基本无关，会稍有变化。这个就是恒磁通的概念。

为了计算方便，我们在这里认为$-\dot{E_1}$也是一个由$I_0$引起的压降，与之对应的，就可以引出励磁阻抗，励磁电流，励磁电感这几个物理量。

\[ -\dot{E_1}=\dot{I_0}Z_{m}=\dot{I_0}\left(r_{m}+jx_{m}\right) \]

励磁电阻抗：$Z_m=r_m+jx_m$
励磁电阻：$r_m$
励磁电抗：$x_m$

上面的物理量是有自己的物理意义的：

$x_m$：励磁电感，反映的是主电抗，大电感。
$r_m$：励磁电阻，反映的是铁耗。

空载的时候电压和电流吸收能量，以补偿铁损和铜损。经过推导，可以得到：

\[ \begin{align*} \dot{U_1} &= -\dot{E_1} + \dot{I_0}Z_1\\ \dot{U_1}\dot{I_0} &= -\dot{E_1}\dot{I_0} + \dot{I_0}^2Z_1\\ p_{Fe} &= -\dot{E_1}\cdot\dot{I_0}\\ &=-\dot{E_1}\cdot \left(\dot{I_\mu}+\dot{I_{Fe}}\right)\\ &=E_1I_{Fe} \end{align*} \]

变压器的负载运行

在上一节中，我们提到了恒磁通的概念，也就是变压器原边的$E_1\approx U_1=const$而且$\phi_m \approx const$。既然主磁通是恒定的，根据基尔霍夫第二定律，我们可以得到总磁势是恒定的。

关键

磁动势恒定是由恒磁通以及忽略漏磁得来的，这个关系式让我们建立了负载电流与空载电流之间的联系。

所以根据这个式子，就可以列出一个很重要的关系式：

\[ \begin{align*} \dot{I_1}N_1 + \dot{I_2}N_2 &= \dot{I_0}N_1 \\ \dot{I_1} + \frac{1}{k} \dot{I_2} &= \dot{I_0} \end{align*} \]

令这个关系式中，$\dot{I_1}=\dot{I_0}+\dot{I_L}$，简单推一下就可以得到

\[ \begin{cases} \dot{I_L}N_1 + \dot{I_2}N_2 = 0\\ \dot{I_2} = -k\dot{I_L} \end{cases} \]

结论：

原副边电流是有联系的。
加上负载以后，原边电流上升很多，符合能量守恒。

接下来分析副边的电压和功率，因为比较简单，所以直接给出结论：

副边的电压：$U_2\approx E_2$

副边的功率：

\[ \begin{align*} p_2 &= \dot{U}_2\dot{I}_2 \approx \dot{E}_2 \left(-k\dot{I}_{1L} \right)\\ &= \left(-\dot{E}_1 \right)\left(-\dot{I}_{1L} \right) \approx \dot{U}_1 \dot{I}_{1L}\\ &= \dot{U}_{1}\dot{I}_{1} - \dot{U}_{1}\dot{I}_{0} \end{align*} \]

结论：

副边绕组的能量来自原边绕组从电网吸收后再传递，传递者就是主磁通。

以后，我们用 $I_m$ 来代替 $I_0$ 表示空载电流。

折算，等效电路，标幺值

后面的知识点，比如折算，等效电路，标幺值都比较简单（如果充分理解了前面的推导的话），所以这里就不再多写。

需要注意的是，最简等效电路常常用于定性分析，在定量计算的时候不要用。

为了更好的理解，建议自己根据方程画一下T型等效电路的相量图。

这里再加一个公式

\[ \alpha = \tan^{-1}\frac{r_m}{x_m} \]

这也是$\alpha$被称作铁损角的原因，其大小主要取决于铁损电阻。

变压器的参数测定

注意

变压器的空载损耗就是铁损。
空载电压的时候是电压加在低压方。
空载实验用T型等效电路
空载实验看电压。
短路实验是电压加在高压方
短路实验看电流。
短路损耗就是铜损。
短路的时候用最简化等效电路。